As discussed briefly in Section 4.1, the problem we are facing when searching for stationary values of the action given in equation (4.1) is optimization; i.e. trying to locate the stationary values. In literature treating the AVP, only minimum and saddle points have been searched for, indicating that there are no maximum points for the action. I will therefore only discuss minimum (both global and local) and saddle points in this thesis. The choice of optimizing methods is a reflection of this; with the exception of the Newton-Raphson method, all of the methods search for stationary values in a descent direction. This automatically excludes any possible maximum points. The Newton-Raphson method is capable of locating any stationary point, but, as we will see in the next chapter, there will solely be minimum and saddle points that are solutions to the action.
A general description of several optimizing methods will be given in this section, while in the next chapter, they will be evaluated by applying them to a system galaxies. The methods will be judged on the ground of effectiveness and ability to locate different solutions. The reason for doing this rather detailed testing is simply that there, as of today, is no method that is known to be better than any other for general use, and that it is hard to say from just looking at the problem which method is best suitable. A description of the methods presented can be found in textbooks like Press,Walsh,DS,GMW,Bert.
In the general treatment given in the remaining parts of this chapter, the function for
which we try to find the minima are referred to as 
, where 
are the
unknown variables. An unconstrained optimization procedure starts by choosing a starting
point; i.e. an initial guess for the values of the unknown parameters in ,
. A substantial amount of computing time can be saved, and the possibility of
actually finding minima increased, by choosing with some care. This means in
practice using whatever information available on the behavior of , so that
our initial guess is not too far from the stationary point(s).
Once the initial point is chosen, we must make two decisions before the next point can be generated: (i) we must first pick a direction along which the next point is to be chosen, and (ii) we must decide on a step size to be taken in that chosen direction. We then have the following iterative picture
where 
is the direction and 
is the step
size. The different optimization methods presented differ in the choice of
and 
. Roughly speaking, we can classify these methods into three
categories:
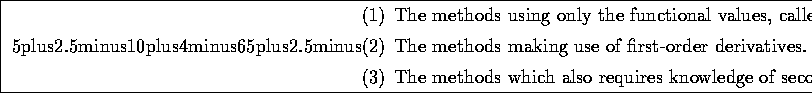The two last categories are often also classified as gradient methods. In
choosing a method, accuracy and especially computing time are of the essence. Category
(1) will not be considered here; it is generally accepted that one should make use of
first-order derivatives if they are available and not too elaborate to calculate.
Category (3) will generally generate points that are sufficiently close to the minimum
point in the least number of steps, but that does not necessarily mean that it is the
most efficient. The computational costs of computing and handling the second derivatives
can be so substantial, that the evaluation of the first derivative alone at several
points would take less computing time. Methods of category (2) would then be a
preferable choice.
For illustrative purposes, a quadratic function will be used in the presentation of these optimizing methods, much due to its simplicity, but mainly because several of these methods where originally designed to solve problems equivalent to minimizing a quadratic function. The n-dimensional quadratic functions used here is on the form
where 
is a positive definite matrix
, and 
are vectors, and c is a scalar constant. The
illustrations presented are 2-dimensional representation of the quadratic, where the
contours represent where the function values are the same.
Let us now take a closer look at some of these optimizing methods, starting with category (2).
