The foregoing method is not self-starting, so a separate initial routine is used to start
the process. From the initial conditions 
, the respective
Taylor series derivatives are formed by successive differentiation of equation
(5.15), analytically. Having calculated the force and derivatives for
each particle, the divided differences to third order and the time-steps are determined,
and the main program is started with these quantities as if they had been obtained by
the main program itself.
Since each particle is assigned its own time-step, the integration cycle itself begins
by determining the next particle i to be advanced, which is the one with the minimum
time-step. The coordinates and velocities of this particle are then determined to
order 
by using equations (5.16) and (5.17), whereupon
the current force may be obtained by direct summation. At this stage, the four past time
epochs are updated to be consistent with the definition that 
denotes the most
recent force evaluation. New differences are now formed, including 
. Together
with the new 
, these correction terms are combined to improve the
current coordinates and velocities to highest order, whereupon the primary coordinates
are initialized by 
.
New time-steps are assigned initially for all particles and at the end of each integration cycle for particle i. The cycle is then repeated on the particle which now has the minimum time-step.
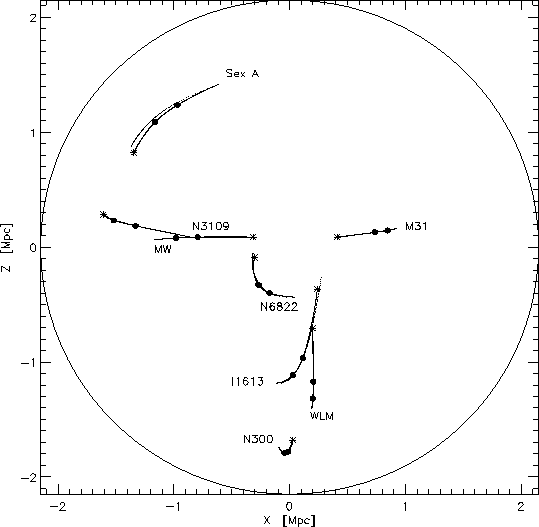
Figure: Action trajectories for 8 galaxies in the LG and the LN (solid
lines), including N-body orbits (dotted lines). Cf. Figure 5.1.
In order to be able to compare the N-body orbits with the the AVP solution, the physical coordinates of the NBODY1 trajectories needs to be transformed into comoving coordinates. Since each positions in NBODY1 is given at time t, the expansion parameter at that time has to be determined. This was done by solving (3.33) for each time t, using the Runge-Kutta method. The code for this subroutine is given in Appendix B.