When developing the AVP code, I compared with work done by others to see whether I arrived at similar solutions of the equations of motion. It was comforting to see that I managed to recreate the solutions given by P-89, which will be the topic of this subsection. Comparing with earlier work is of course not enough to confirm the validity of the solutions--I therefore checked the solutions using the N-body code, which will be dealt with in Section 5.2.
To be able to fully compare the solutions from the AVP code with those from
P-89, it is essential to make use of the same conditions and methods. Peebles
used an optimizing method which he referred to as ``walking down the gradient'', which
is equivalent to the method of Steepest Descent from Section 4.3.
As we have seen, this method will most likely lead to a slow
convergence, so in order to avoid the calculations spending too long computing time, the
iterative process is stopped in due time before machine accuracy is reached. The
termination is set to 
, where the coefficients on average
are accurate to about the second decimal point, which in turn gives the resulting
positions in about five decimal digits accuracy.
Since the only motive here is to get an indication if the AVP does what it is
designed to do, the system with the least number of variables used by P-89 was
chosen. Hopefully this will save us some computing time. This system consist of 8
galaxies in the LG and the LN: the MW, M31 and 6 dwarf galaxies, where the mass of M31
is adjusted to be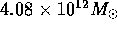 
. Detailed properties of each individual
mass tracer is given in Table 5.1, equivalent to Table 1 in Peebles' paper.
Quite a few of these properties have later been modified, but for the sake of comparison,
they will be applied here (and in Section 5.3). The cosmology is given by
and h=0.84, and the trial functions used are given in equation
(3.22), with N=5. The resulting system consists of 120 unknown variables,
which is usually considered as a relatively modest size. The integration of the action
and its first derivatives were approximated by 15 points in time using the Gaussian
Quadrature method.
Table 5.1: Eight galaxies in the LG and the LN. The columns are: (1) common
name, (2,3) celestial coordinates (1950), (4) distance from the Milky Way, (5) mass
relative to the mass of M31, (6) mass when 
[cf.][]P-89, and (7) redshift referred to the centre of the Milky Way
[data from][]P-95.
The search for the minima is started at the point 
, and continues in
the direction of the negative gradient. The step length is not determined by linear
search, since such a search would include numerous calculations of both the action and
its derivative, and hence spend a long computing time. Instead, an initial step length
is given, which during the iterative process is modified so that the action is reduced
at each iteration. It will be shown later that this rather crude method is indeed to be
preferred over linear searches (Section 5.3).
The calculations confirm what was indicated in Subsection 4.3.1, that the
Steepest Descent method has initially a very fast convergence, which slows down as the
solution is approached. Driving the norm of the gradient toward 
goes fairly quickly, 
CPU-seconds, while reaching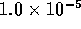 
takes
a lot longer,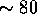 
CPU-seconds. This indicates that we are dealing with a very
badly scaled system. Improvements can be made, which will be discussed in Section
5.3.
Figure 5.1: Action trajectories for 8 galaxies in the LG and the LN, plotted
in comoving coordinates. The orbits are projected into the xz-plane, and the labels
are placed near the initial position of the mass tracers. The circle has radius
Mpc. Cf. P-89.
The resulting coefficients are used to calculate the orbits of each mass tracer and
their respective physical velocities at times a=0.01 and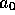 
, whereupon the orbits
were plotted using IDL (Interactive Data Language), see Figure 5.1. Comparing
this plot to Figure 1 given by P-89, should indicate that we have both arrived
at the same solution. The orbits are not just visually similar, also the present radial
velocity matched well with the result given by Peebles, see Table 5.2. For
comparison, the observed radial velocities are also given in Table 5.2, and
their values are in good agreement with both Peebles' result and the solution from
AVP. The reason for the rather large discrepancy for the solution of NGC 6822 is
discussed in Section 6.1.
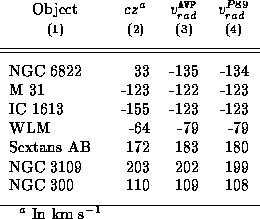
Table 5.2: Radial velocities for 7 galaxies in the LG and the LN. The
columns are: (1) common name, (2) observed radial velocities based on redshift
[data from][]P-95, (3) radial velocities from AVP, and (4) radial
velocities from [][solution 1]P-89.
Some details about the presentation of the solutions, as in Figure 5.1,
follows. The orbits are plotted in comoving coordinates, and the circle represents the
radius, 
, of the sphere that would contain the total mass of the mass tracers in
the plot, 
, if the mass density was homogeneous (see equation 3.36). The
plots are projections of the solution orbits into the xz-plane in Cartesian
coordinates given in equation (5.3). As mentioned in the previous subsection,
the coordinate system needs to be rotated in order to be able to compare them to those of
P-89. The rotation results in the x-axis pointing along the line from the MW
to M31 at their current positions, i.e. in the direction 
.
The orthogonal y-axis is then at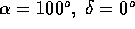 
and the orthogonal
z-axis at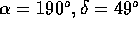 
. This rotation is applied throughout this thesis.
The labels are near the initial position at a=0.01, and the star symbols represent the
present positions of the mass tracers. The filled circles show the comoving position at
redshift z=3 and z=1.
Searches with several different initial values for the coefficients has failed to reveal other solutions than the one presented in Figure 5.1. It will be shown in Section 5.3 that there indeed are other solutions that gives a stationary action, it is just that the Steepest Descent fails to locate them.